slendr crash course


You can use this document as a cheat sheet as you work on the exercises. It contains everything you need to know about slendr, in a compressed form.

Typical slendr workflow

We will always start our R scripts with this:

library(slendr) # You can safely ignore any potential warnings!
init_env()      # This activates the internal Python environmet


Followed by some combination of the following:

  1. creating populations
  2. programming \(N_e\) size changes
  3. encoding gene-flow events
  4. simulating genomic data
  5. computing popgen statistics

Creating populations

At minimum, we need its name, size and “time of appearance”:

pop1 <- population("pop1", N = 1000, time = 1)

This creates a normal R object! Typing it out gives a summary:

pop1
slendr 'population' object 
-------------------------- 
name: pop1 
non-spatial population
stays until the end of the simulation

population history overview:
  - time 1: created as an ancestral population (N = 1000)

Note: Because slendr uses either msprime or SLiM internally for simulation of genomic data, all individuals are assumed to be diploid.

Programming population splits

Splits are defined by providing a parent = <pop> argument:

pop2 <- population("pop2", N = 100, time = 50, parent = pop1)

Note: Here pop1 is an R object created above, not a string "pop1"!

The split is again reported in the “historical summary”:

pop2
slendr 'population' object 
-------------------------- 
name: pop2 
non-spatial population
stays until the end of the simulation

population history overview:
  - time 50: split from pop1 (N = 100)

Scheduling resize events

  • Step size decrease:
pop1 <- population("pop1", N = 1000, time = 1)
pop1_step <- resize(pop1, N = 100, time = 500, how = "step")
  • Exponential increase:
pop2 <- population("pop2", N = 100, time = 50, parent = pop1)
pop2_exp <- resize(pop2, N = 10000, time = 500, end = 2000, how = "exponential")

Tidyverse-style pipe %>% interface

The following leads to a more concise (and “elegant”) code.

  • Step size decrease:
pop1 <-
  population("pop1", N = 1000, time = 1) %>%
  resize(N = 100, time = 500, how = "step")
  • Exponential increase:
pop2 <-
  population("pop2", N = 1000, time = 1) %>%
  resize(N = 10000, time = 500, end = 2000, how = "exponential")

Note: You can read (and understand) a() %>% b() %>% c() as “take the result of the function a, pipe it into function b, and then pipe that to function c”.

A more complex model

Using just the two functions introduced so far:

pop1 <- population("pop1", N = 1000, time = 1)

pop2 <-
  population("pop2", N = 1000, time = 300, parent = pop1) %>%
  resize(N = 100, how = "step", time = 1000)

pop3 <-
  population("pop3", N = 1000, time = 400, parent = pop2) %>%
  resize(N = 2500, how = "step", time = 800)

pop4 <-
  population("pop4", N = 1500, time = 500, parent = pop3) %>%
  resize(N = 700, how = "exponential", time = 1200, end = 2000)

pop5 <-
  population("pop5", N = 100, time = 600, parent = pop4) %>%
  resize(N = 50, how = "step", time = 900) %>%
  resize(N = 1000, how = "exponential", time = 1600, end = 2200)

Again, each object carries its history!

For instance, this is the summary you will get from the last population from the previous code chunk:

pop5
slendr 'population' object 
-------------------------- 
name: pop5 
non-spatial population
stays until the end of the simulation

population history overview:
  - time 600: split from pop4 (N = 100)
  - time 900: resize from 100 to 50 individuals
  - time 1600-2200: exponential resize from 50 to 1000 individuals

This way, you can build up complex models step by step, checking things as you go by interacting with the R console.

Gene flow / admixture

We can schedule gene flow from pop1 into pop2 with:

gf <- gene_flow(from = pop1, to = pop2, start = 2000, end = 2200, rate = 0.13)

Note: Here rate = 0.13 means 13% migrants over the given time window will come from “pop1” into “pop2”.


Multiple gene-flow events can be gathered in a list:

gf <- list(
  gene_flow(from = pop1, to = pop2, start = 500, end = 600, rate = 0.13),
  gene_flow(from = ..., to = ..., start = ..., end = ..., rate = ...),
  ...
)

Model compilation


This is the final step before we can simulate data.


model <- compile_model(
  populations = list(pop1, pop2, pop3, pop4, pop5),
  generation_time = 1,       # (converts the all times into generations)
  simulation_length = 3000,  # (number of generations to run the simulation for)
  direction = "forward"      # (not totally necessary but good practice)
)


compile_model() takes a list of components, performs some consistency checks, and returns a single R object

Model compilation


This is the final step before we can simulate data.


model <- compile_model(
  populations = list(pop1, pop2, pop3, pop4, pop5),
  gene_flow = gf,      # <----- in case our model includes gene flow(s)
  generation_time = 1,
  simulation_length = 3000,
  direction = "forward"
)


Gene flow(s) can be included via the gene_flow argument.

Model summary

Typing the compiled model into R prints a brief summary:

model
slendr 'model' object 
--------------------- 
populations: pop1, pop2, pop3, pop4, pop5 
geneflow events: 1 
generation time: 1 
time direction: forward 
time units: generations 
total running length: 3000 time units
model type: non-spatial

configuration files in: /private/var/folders/h2/qs0z_44x2vn2sskqc0cct7540000gn/T/RtmpIAAt4D/file73db217b5999_slendr_model

This can be useful as a quick overview of the model we are working with. However, a better way to check a model is…

Model visualization

plot_model(model)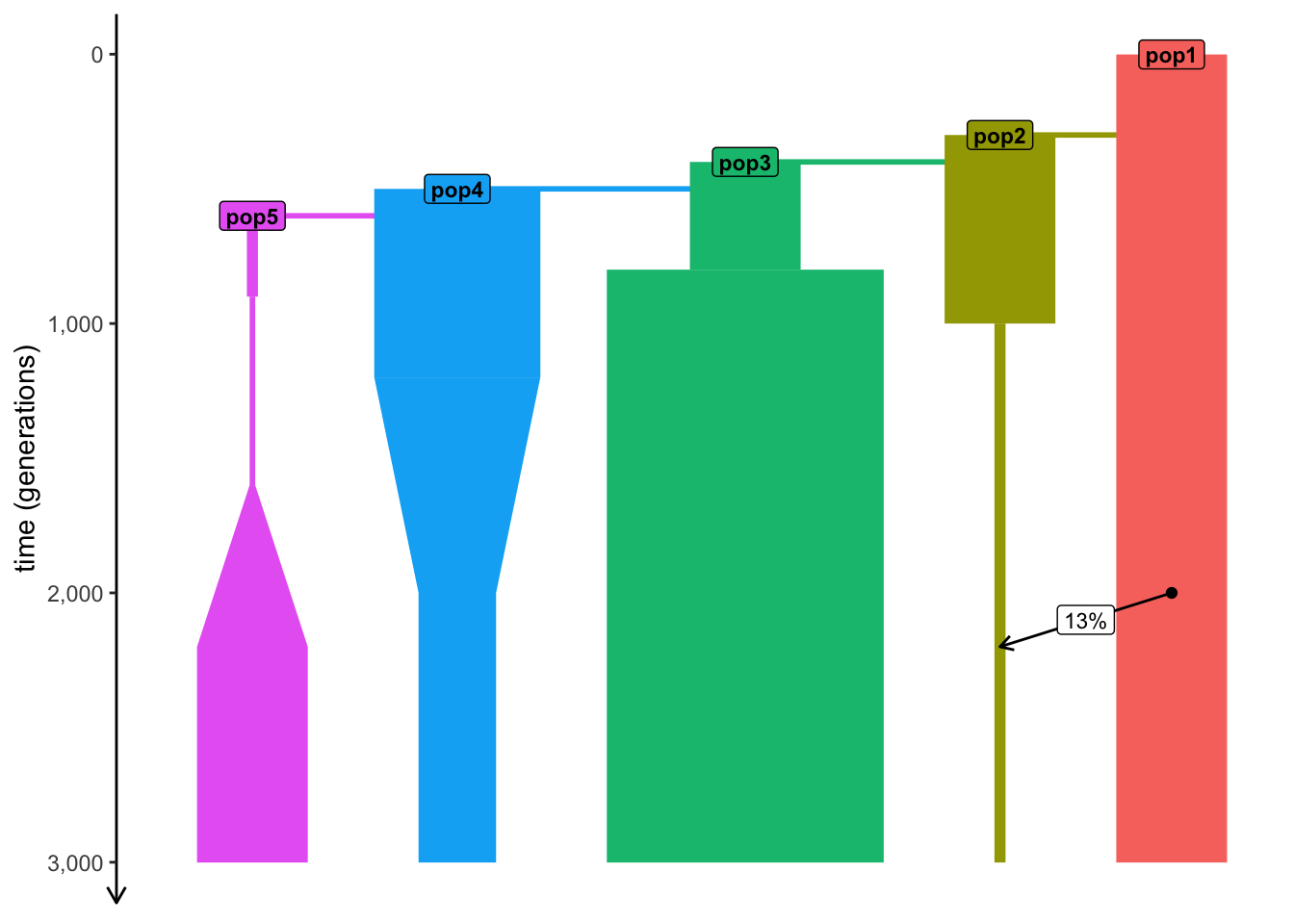

A note on units of time (and its direction)


Sometimes you want to work with time units such as “years ago” (aDNA radio-carbon dated samples, etc.), but you have to convert those to “generations forward” for some software.

slendr helps by making it possible to use whatever time units or time directions are more natural for a particular project.

“Forward time units”

pop1 <- population("pop1", N = 1000, time = 1)

pop2 <-
  population("pop2", N = 1000, time = 300, parent = pop1) %>%
  resize(N = 100, how = "step", time = 1000)

pop3 <-
  population("pop3", N = 1000, time = 400, parent = pop2) %>%
  resize(N = 2500, how = "step", time = 800)

pop4 <-
  population("pop4", N = 1500, time = 500, parent = pop3) %>%
  resize(N = 700, how = "exponential", time = 1200, end = 2000)

pop5 <-
  population("pop5", N = 100, time = 600, parent = pop4) %>%
  resize(N = 50, how = "step", time = 900) %>%
  resize(N = 1000, how = "exponential", time = 1600, end = 2200)

model <- compile_model(
  populations = list(pop1, pop2, pop3, pop4, pop5),
  generation_time = 1,
  simulation_length = 3000, # forward-time sims need an explicit end
  direction = "forward"
)

We started with pop1 in generation 1, with later events at an increasing time value.

“Forward time units”

plot_model(model) # see time progressing from generation 1 forwards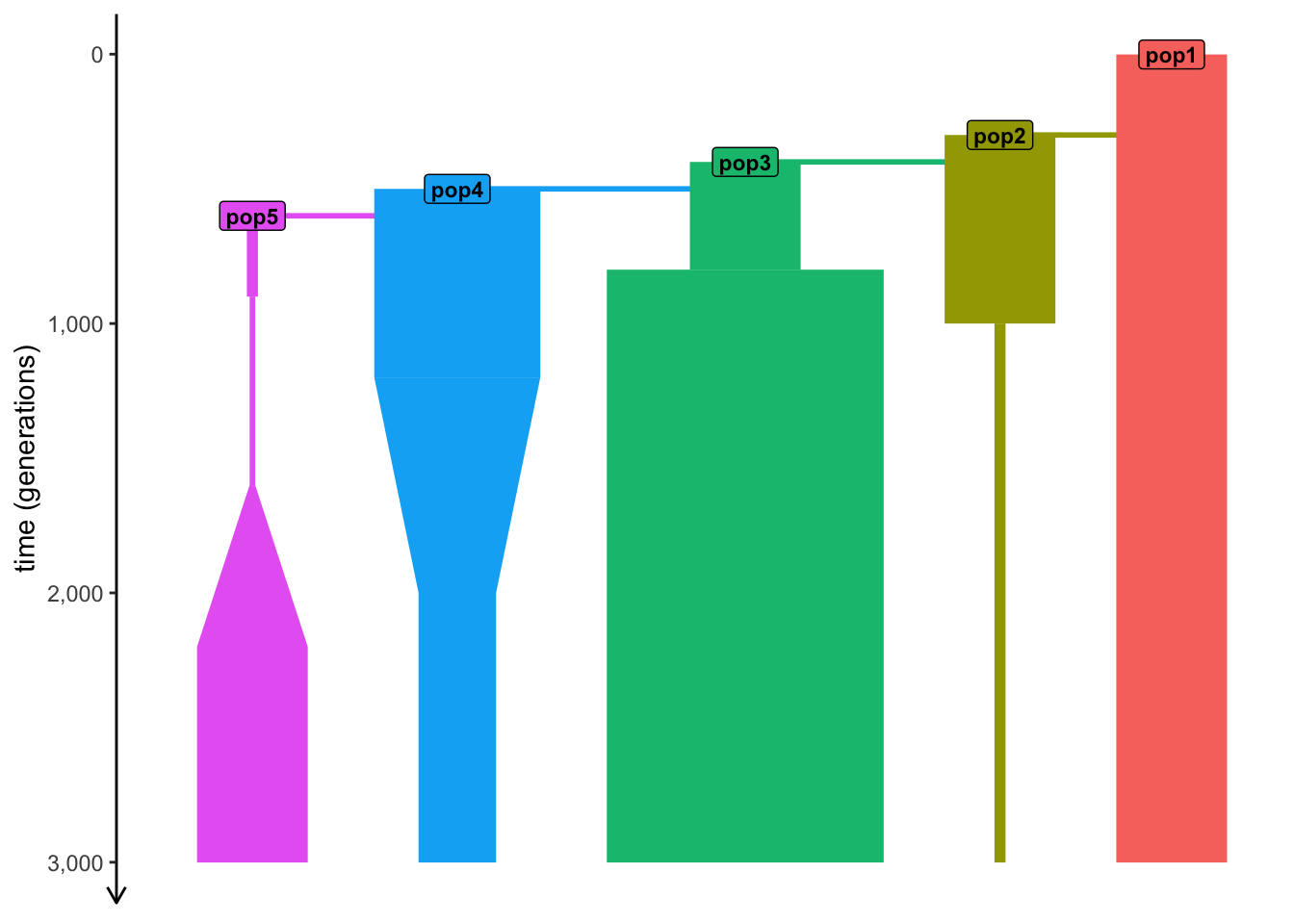

We started with pop1 in generation 1, with later events at an increasing time value.

“Backward time units”

pop1 <- population("pop1", N = 1000, time = 30000)

pop2 <-
  population("pop2", N = 1000, time = 27000, parent = pop1) %>%
  resize(N = 100, how = "step", time = 20000)

pop3 <-
  population("pop3", N = 1000, time = 26000, parent = pop2) %>%
  resize(N = 2500, how = "step", time = 22000)

pop4 <-
  population("pop4", N = 1500, time = 25000, parent = pop3) %>%
  resize(N = 700, how = "exponential", time = 18000, end = 10000)

pop5 <-
  population("pop5", N = 100, time = 24000, parent = pop4) %>%
  resize(N = 50, how = "step", time = 21000) %>%
  resize(N = 1000, how = "exponential", time = 14000, end = 8000)

model <- compile_model(
  populations = list(pop1, pop2, pop3, pop4, pop5),
  generation_time = 10 # (10 time units for each generation)
  # (we don't need to provide `simulation_length =` because
  # "backwards" models end at time 0 by default, i.e. "present-day")
)

Same model as before, except now expressed in units of “years before present”.

“Backward time units”

plot_model(model) # see time progressing from "year" 30000 backwards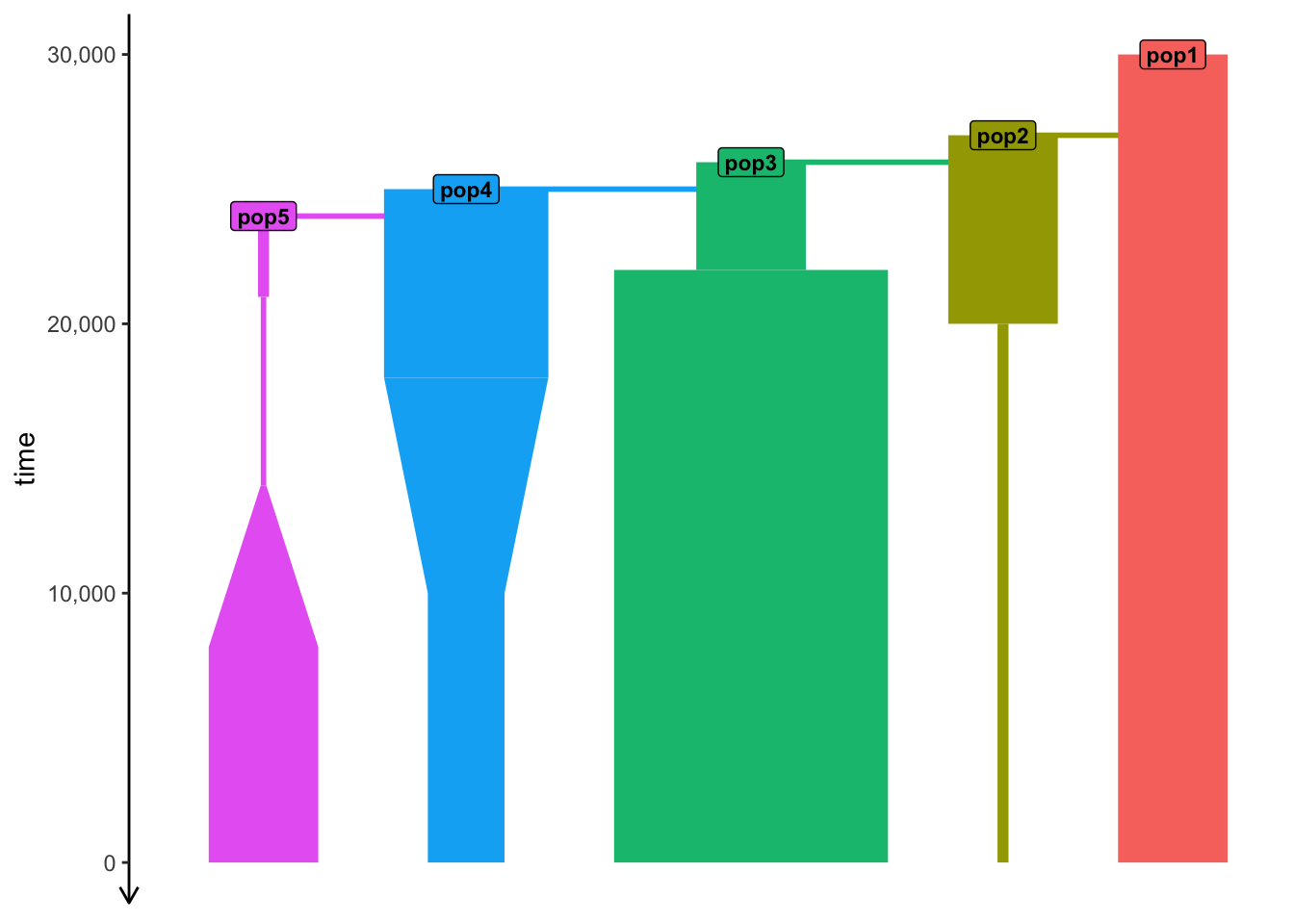

Same model as before, except now expressed in units of “years before present”.

So we built a model…

… but how do we simulate data from it?

Built-in simulation “engines”

slendr has two simulation “engine scripts” built-in:

They are designed to “understand” slendr models, meaning that you can simulate data just with this command:

ts <- msprime(model, sequence_length = 10e6, recombination_rate = 1e-8)


No need to write any msprime or SLiM code!

The result of a simulation is a tree sequence (ts)

What is tree sequence?

  • a record of full genetic ancestry of a set of samples
  • an encoding of DNA sequence carried by those samples
  • an efficient analysis framework

Why tree sequence?


Why not VCF or a normal genotype table?

What we usually have

What we usually want

An understanding of our samples’ evolutionary history:

This is exactly what a tree sequence is!

Image from the tskit documentation

The magic of tree sequences

They allow us to compute statistics without genotypes!

There is a “duality” between mutations and branch lengths.

Note: See an amazing paper by Ralph et al. (2020) for more detail.

What if we need mutations though?

 

What if we need mutations though?

Coalescent and mutation processes can be decoupled!

This means we can add mutations to ts after the simulation using ts_mutate().

Let’s go back to our example model…

plot_model(model)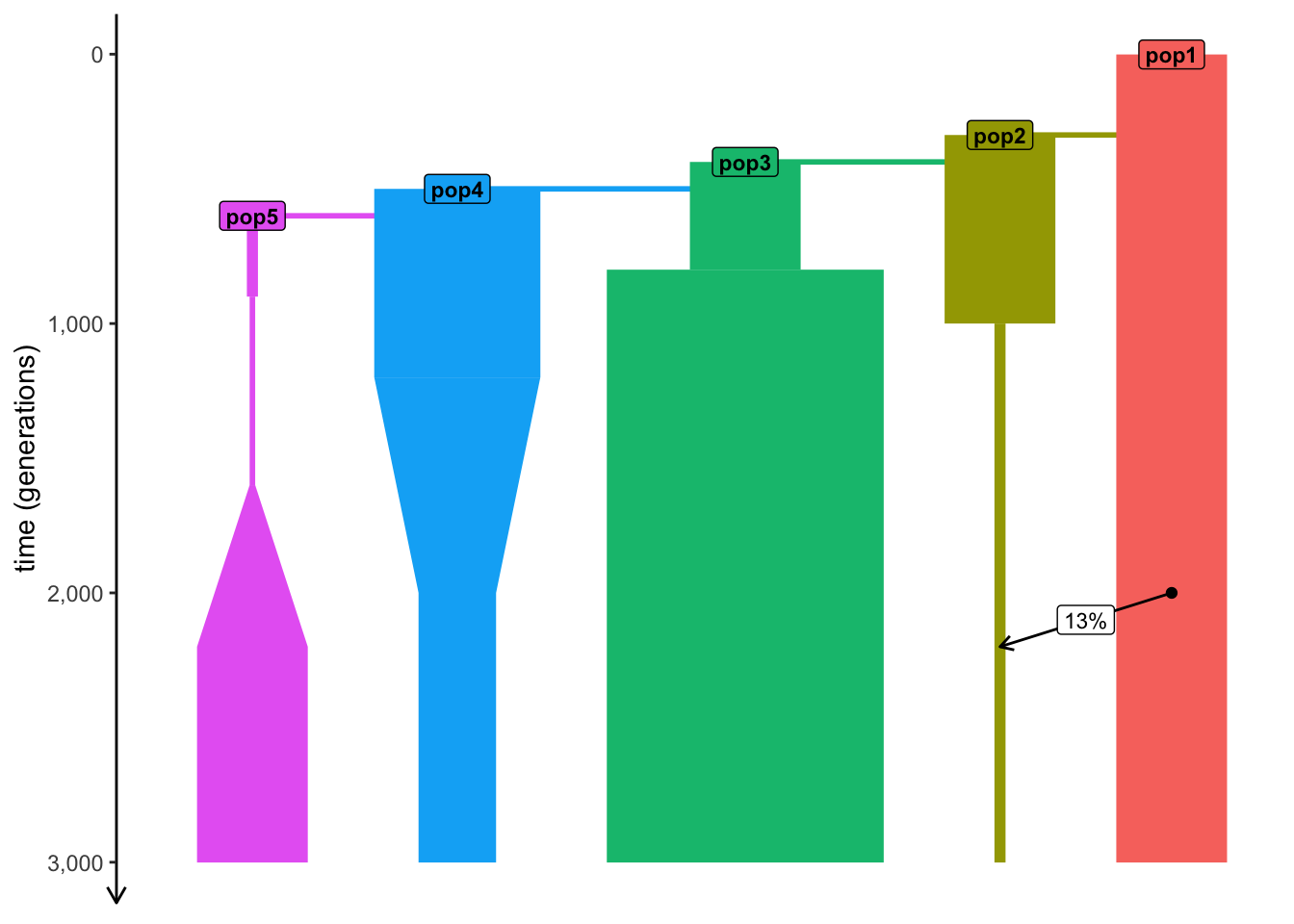

… simulate a tree sequence…


In our script we’ll have something like this:

library(slendr)
init_env()

# <... population() definitions ...>

# <... gene_flow() definition ...>

# <... compile_model(...) ...>
  
ts <-
  msprime(model, sequence_length = 50e6, recombination_rate = 1e-8)

… and overlay mutations on it


In our script we’ll have something like this:

library(slendr)
init_env()

# <... population() definitions ...>

# <... gene_flow() definition ...>

# <... compile_model(...) ...>
  
ts <-
  msprime(model, sequence_length = 50e6, recombination_rate = 1e-8) %>%
  ts_mutate(mutation_rate = 1e-8)
Note: In some exercises, mutations won’t be necessary. Where we will need them, you can use ts_mutate() using the pattern shown here.

So we can simulate data

How do we work with this ts thing?

slendr’s R interface to tskit statistics

Allele-frequecy spectrum, diversity \(\pi\), \(F_{ST}\), Tajima’s D, etc.

Find help at slendr.net/reference or in R under ?ts_fst etc.

Extracting names of recorded samples

  1. We can get individuals recorded in ts with ts_samples():
ts_samples(ts) %>% head(1) # returns a data frame (one row here, for brevity)
    name time  pop
1 pop1_1 3001 pop1
  1. A shortcut ts_names() can also be useful:
ts_names(ts) %>% head(5) # returns a vector of individuals' names
[1] "pop1_1" "pop1_2" "pop1_3" "pop1_4" "pop1_5"
  1. We can get a per-population list of individuals like this:
ts_names(ts, split = "pop") # returns a named list of such vectors
$pop1
[1] "pop1_457" "pop1_917" "pop1_654" "pop1_23"  "pop1_219"

All slendr statistics take individuals’ names as their function arguments.


This is modelled after the sample_sets= argument of the respective tskit Python methods (except you use names of individuals directly, not tree-sequence node numbers).

Let’s take a look at how it works in general…

tskit computation – option #1

For a function which operates on one set of individuals, we can first get a vector of names to compute on like this:

# a random selection of names of three individuals in a tree sequence
samples <- c("popX_1", "popX_2", "popY_42")


Then we can calculate the statistic of interest like this:

# this computes nucleotide diversity in our set of individuals
df_result <- ts_diversity(ts, sample_sets = list(samples))

Note: Wherever you see list(<vector of names>), you can think of it as “compute a statistic for the entire group of individuals” (you get a single number). Without the list(), it would mean “compute the statistic for each individual separately” (and get a value for each of them individually).

tskit computation – option #2

For a function operating on multiple sets of individuals, we want a list of vectors of names (one such vector per group):

# when we compute on multiple groups, it's a good idea to name them
samples <- list(
  popX = c("popX_1", "popX_2", "popX_3"),
  popY = c("popY_1", "popY_2", "popY_3"),
  popZ = c("popZ_1", "popZ_2")
)


Then we use this list of vectors in the same way as before:

# this computes a pairwise divergence between all three groups
df_result <- ts_divergence(ts, sample_sets = samples)

tskit computation – option #3

For something like \(f\) statistics, the function arguments must be more precisely specified (here A, B, C, not sample_sets):

df_result <- ts_f3(
  ts,
  A = c("popX_1", "popX_2", "popX_3"),
  B = c("popY_1", "popY_2", "popY_3"),
  C = c("popZ_1", "popZ_2")
)

Doing this manually can be annoying — ts_names() helps by preparing the list of names in the correct format:

# get names of individuals in each population as a named list of vectors
samples <- ts_names(ts, split = "pop")

# use this list directly by specifying which vectors to take out
ts_f3(ts, A = samples$popX, B = samples$popY, C = samples$popZ)

Some examples on simulated data


(A tree sequence ts we got earlier.)

Example: nucleotide diversity

Get a list of individuals in each population:

samples <- ts_names(ts, split = "pop")

names(samples)
[1] "pop1" "pop2"


We can index into the list via population name:

samples$pop1
[1] "pop1_1" "pop1_2" "pop1_3"
samples$pop2
[1] "pop2_1" "pop2_2" "pop2_3"

 

Compute nucleotide diversity (note the list samples):

ts_diversity(ts, sample_sets = samples)
# A tibble: 2 × 2
  set   diversity
  <chr>     <dbl>
1 pop1  0.000406 
2 pop2  0.0000707


Our tree sequence had two populations, pop1 and pop2, which is why we get a data frame with diversity in each of them.

Example: allele frequency spectrum

Get names of individuals:

samples <- ts_names(ts)[1:5]
samples
[1] "pop_1" "pop_2" "pop_3" "pop_4" "pop_5"

Compute the AFS:

afs <- ts_afs(ts, sample_sets = list(samples))

# we skip the 1st item because it has a special meaning in tskit
afs[-1]
 [1] 3917 2151 1432  941  740  624  607  587  416  385

 

plot(afs[-1], type = "b",
     xlab = "allele count bin",
     ylab = "frequency")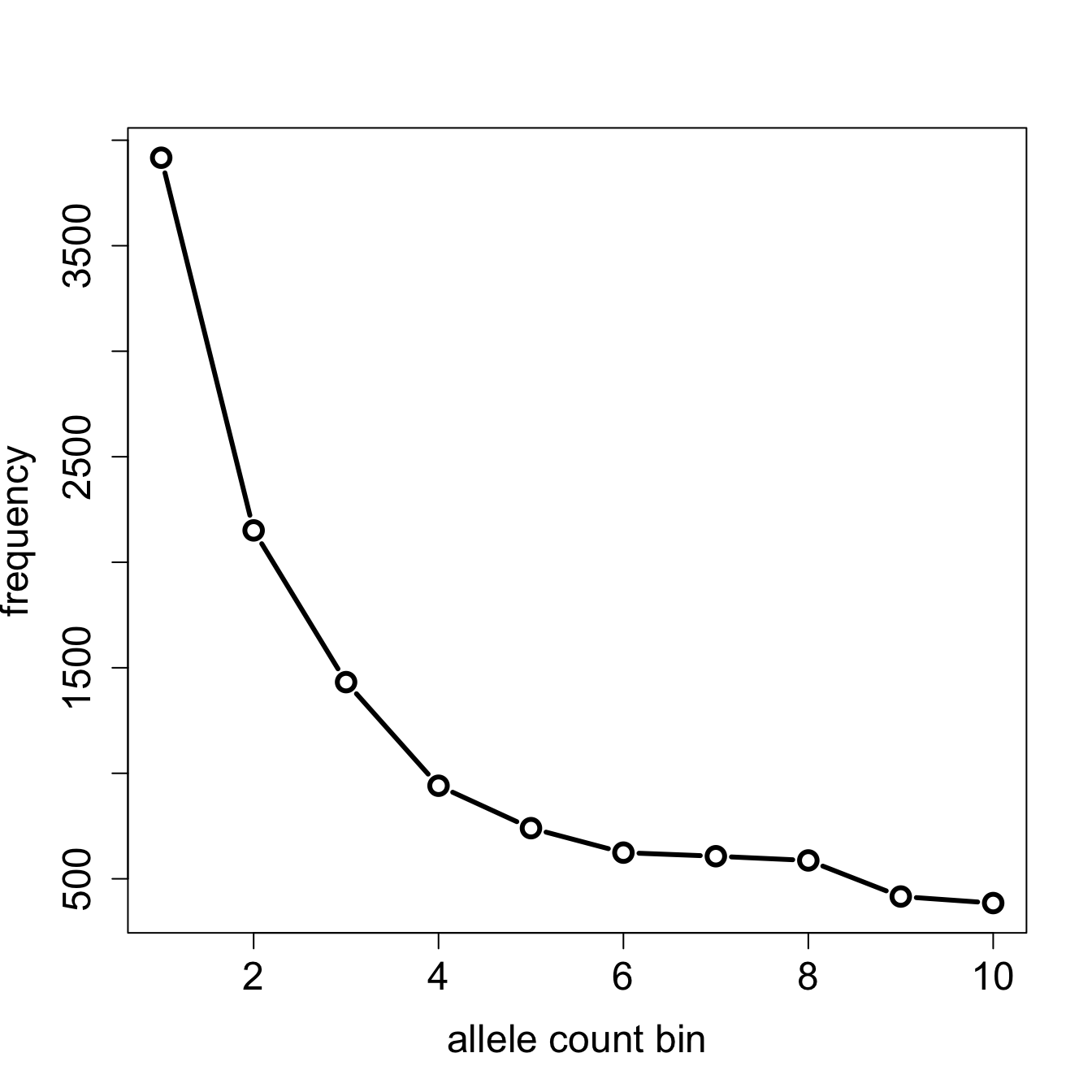

Note: One of the rare examples when a slendr / tskit statistical function does not return a data frame (ts_afs() returns a numerical vector, not a data frame).

More details on tree-sequences

Tree sequence tables


This simulates 2 \(\times\) 10000 chromosomes of 100 Mb:

library(slendr)
init_env(quiet = FALSE)

pop <- population("pop", time = 100e6, N = 10000)
model <- compile_model(pop, generation_time = 30, direction = "backward")
ts <- msprime(model, sequence_length = 1e6, recombination_rate = 1e-8)
The interface to all required Python modules has been activated.


Runs in less than 30 seconds on my laptop!

Takes only about 66 Mb of memory!

How is this even possible?!

Tree-sequence tables

A tree can be represented by

  • a table of nodes,

  • a table of edges between nodes,

  • a table of mutations on edges


A collection of such tables is a tree sequence.

Note: This is a huge oversimplification. Find more information in tskit docs.

Tree-sequence tables in practice

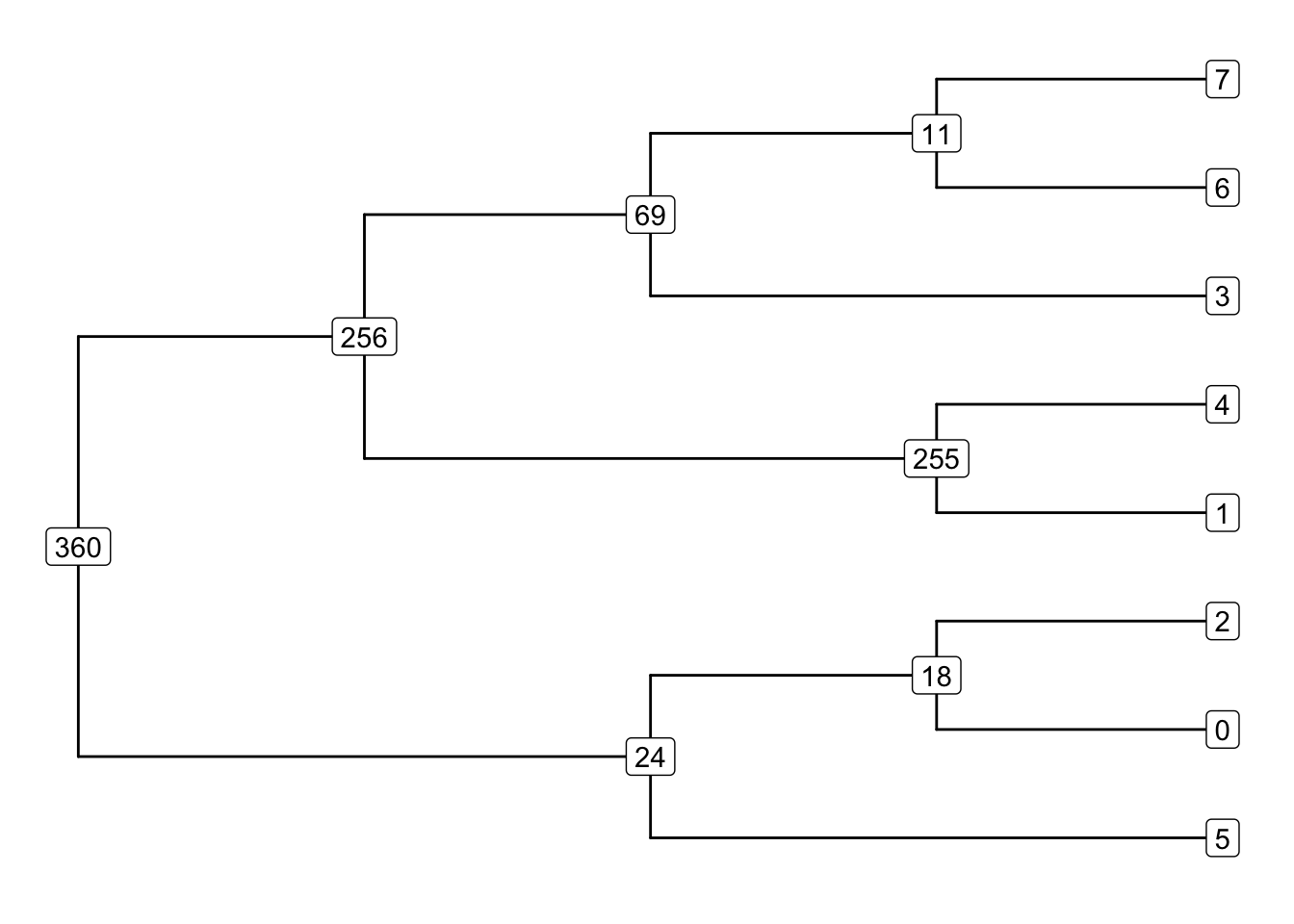
Nodes:

  node     time
1  360 871895.1
2  256 475982.3
3  255 471179.5

Edges:

  child parent
1   256    360
2   255    256
3    69    256

Mutations:

   id node     time
1  69   74 125539.4
2 272   22 242337.9
3 277   22 129474.1

Other data formats


Tree sequence is a useful, cutting-edge data structure, but there are many well-established bioinformatics tools out there.


tskit and slendr offer a couple of functions to help integrate their simulation results into third-party software.

Standard genotype formats

If a tree sequence doesn’t cut it, you can always…

  • export genotypes to a VCF file:
ts_vcf(ts, path = "path/to/a/file.vcf.gz")
  • export genotypes in the EIGENSTRAT format:
ts_eigenstrat(ts, prefix = "path/to/eigenstrat/prefix")
  • access genotypes as a data frame:
ts_genotypes(ts)
    pos pop_1_chr1 pop_1_chr2 pop_2_chr1 pop_2_chr2 pop_3_chr1 pop_3_chr2
1 12977          0          1          0          0          0          0
2 15467          1          0          1          1          1          1